Numerous sophisticated tools currently exist that allow for the deployment of meta-algorithms in a global optimization context (Pyomo, AMPL, etc.). These tools are generally built on advanced modeling languages (AMLs) and rely on well-developed optimization routines to solve subproblems [1,2]. However, this accessibility comes at a cost. Lower-level optimization routines become obscured; as a result, a substantial barrier exists to the development novel optimization approaches. Moreover, not all engineering systems can be readily described using the syntax available in standard AMLs.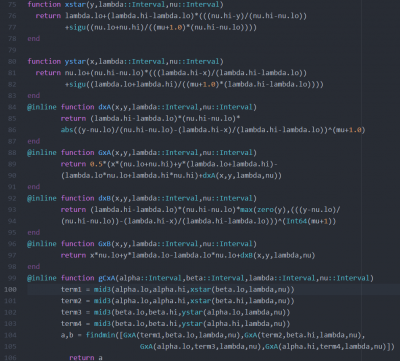
With these limitations in mind, we’ve developed the EAGO research platform [3]. This software application consists of a series of modular low-level components common in global optimization routines. By utilizing the Julia computing language [4], the workflow required to test novel approaches have been greatly streamlined. The abstract syntax tree (AST) nature of Julia allows for stable macro programming and fundamentally different software paradigms, such as aspect-oriented programming, to be readily explored. Current functionality for the EAGO toolset includes:
- A flexible branch-and-bound library.
- A library for the smooth McCormick relaxations presented in [5].
- A JuMP front-end to support model definition in the control, state, and uncertain framework presented in [6].
- Nonconvex global solvers for algorithmically- and AML-defined problems [7,8]
- Routines for solving general nonconvex semi-infinite programs [9,10]
- Feasibility-based bound tightening (FBBT) via interval contractors on directed acyclic graphs (DAG) [11].
- Parametric interval methods for bounding implicit functions [12].
Additional packages are planned to incorporate optimality-based bounds tightening (OBBT) [13], flexible object algebra library, integration with flowsheet tools, standard McCormick relaxations [6,7,8,14]. Learn more about EAGO and download the software at: https://github.com/PSORLab/EAGO.jl.
Research Products:
- Gottlieb, R.X., Xu, P., and M.D. Stuber. Automatic Source Code Generation of Complicated Models For Deterministic Global Optimization With Parallel Architectures. In Proceedings, FOCAPO-CPC 2023, San Antonio, Texas, Jan 9, 2023. (paper)
- Wilhelm, M.E., Wang, C., and M.D. Stuber. Convex and Concave Relaxations of Artificial Neural Network Activation Functions. Journal of Global Optimization. (2022) DOI: 10.1007/s10898-022-01228-x
- Wang, C., Wilhelm, M.E., and M.D. Stuber. Semi-Infinite Optimization with Hybrid Models. Industrial & Engineering Chemistry Research. 61, 5239-5254 (2022). DOI: 10.1021/acs.iecr.2c00113
- Stuber, M.D., Gottlieb, R.X., and Wilhelm, M.E. Global Optimization of Advanced Formulations with EAGO.jl: Recent Advances. In Proceedings, EURO 2022, Helsinki, Finland, Jul 5, 2022.
- Wilhelm, M. E., Gottlieb, R. X., and Stuber, M. D. EAGO.jl: Next Generation Global and Robust Optimization in Julia, Revisited. In Proceedings, AIChE 2021, Boston, MA, Nov 7, 2021.
- Stuber, M. D., and Wilhelm, M. E. Recent Advances in EAGO.jl: A Feature-Rich Global Solver and Research Platform. In Proceedings, INFORMS 2021, Virtual and Anaheim, CA, Oct 25, 2021.
- Wilhelm, M. E., and Stuber, M. D. Reduced-Space Optimization of Data-Driven Hybrid Models in EAGO.jl. In Proceedings, INFORMS 2021, Virtual and Anaheim, CA, Oct 24, 2021.
- Stuber, M. D., and Wilhelm, M. E. Recent Advances in EAGO.jl: Easy Advanced Global Optimization in Julia. In Proceedings, EURO 2021 – 31st European Conference on Operational Research, Athens, Greece, July 13, 2021.
- Wilhelm, M.E., Le, A.V., and M.D. Stuber. Global Optimization of Stiff Dynamical Systems. AIChE Journal. 65(12):e16836 (2019). DOI: 10.1002/aic.16836
- Wilhelm, M.E. and M.D. Stuber. EAGO.jl: Easy Advanced Global Optimization in Julia. Optimization Methods & Software. (2020). DOI: 10.1080/10556788.2020.1786566
- Stuber, M.D. A Differentiable Model for Optimizing Hybridization of Industrial Process Heat Systems with Concentrating Solar Thermal Power. Processes. 6(7), 76 (2018). DOI: 10.3390/pr6070076
- Stuber, M. D. EAGO.jl: Easy Advanced Global Optimization in Julia. In Proceedings, EURO 2019 – 30th European Conference on Operational Research, Dublin, Ireland, Jun 24, 2019.
- Wilhelm, M. and Stuber, M. D. Tightening McCormick Relaxations Via Reformulation of Intermediate Functions into Schema. In Proceedings, AIChE 2018, Pittsburgh, PA, Oct 30, 2018.
- Wilhelm, M. and Stuber, M. D. Quadratic Underestimators of Differentiable McCormick Relaxations for Deterministic Global Optimization. In Proceedings, AIChE 2018, Pittsburgh, PA, Oct 30, 2018.
- Wilhelm, M. and Stuber, M. D. Recent Advances in EAGO: Global and Robust Optimization in Julia, In Proceedings, AIChE 2018, Pittsburgh, PA, Oct 28, 2018.
- Wilhelm, M. and Stuber, M. D. EAGO: A Deterministic Nonconvex Optimization Package for Julia. Second Annual JuMP-dev Workshop. In Proceedings, Second Annual JuMP-Dev Workshop, Bordeaux, France, Jun 29, 2018.
- Wilhelm, M. and Stuber, M. D. Easy Advanced Global Optimization (EAGO): An Open-Source Platform for Robust and Global Optimization in Julia. In Proceedings, AIChE 2017, Minneapolis, MN, Oct 31, 2017.
References
[1] Hart, W. E.; Watson, J.P. & Woodruff, D. L. Pyomo: modeling and solving mathematical programs in Python. Mathematical Programming Computation, 3, 219, 2011
[2] Fourer, Robert, David M. Gay, and Brian W. Kernighan. AMPL: A mathematical programming language. Murray Hill, NJ 07974: AT&T Bell Laboratories, 1987.
[3] Wilhelm, M.E., Stuber, M.D. Easy Advanced Global Optimization (EAGO): An Open-Source Platform for Robust and Global Optimization in Julia. AIChE Annual Meeting, Minneapolis MN, 2017
[4] Bezanson, J. et al. Julia: A fresh approach to numerical computing. SIAM Review. 59, 65-98, 2017.[5] Khan, K.A., Watson, H.A., and Barton, P.I. Differentiable McCormick Relaxations. J Global Optim, 67(4):687-729, 2017.
[6] Halemane, K. P. and Grossmann, I. E. Optimal process design under uncertainty. AIChE Journal. 29, 425-433, 1983
[7] Mitsos, A., Chachuat, B., and Barton, P.I. McCormick-Based Relaxations of Algorithms. SIAM J. Optim. 20(2): 573-601.
[8] Stuber, M.D., Scott, J.K., and P.I. Barton. Convex and Concave Relaxations of Implicit Functions. Optimization Methods and Software. 30(3), 424-460, 2014.
[9] Mitsos, A. Global Optimization of Semi-Infinite Programs via Restriction of the Right-Hand Side. Optimization. 60:10-1,1291-1308, 2011.
[10] Stuber, M.D., and Barton, P.I. Semi-Infinite Optimization with Implicit Functions. Ind. Eng. Chem. Res., 54, 307-317, 2015.
[11] Stuber, M.D., et al. Worst-case design of subsea production facilities using semi-infinite programming. AIChE Journal, 60, 2513-2524, 2014
[12] Stuber, M.D., Evaluation of Process Systems Operating Envelopes. MIT, PhD Thesis, 2012
[13] Gleixner, A. M., et al. Three enhancements for optimization-based bound tightening. Journal of Global Optimization, 67, 731-757, 2017
[14] McCormick, G.P. Computability of global solutions to factorable nonconvex programs: Part I — Convex underestimating problems. Mathematical Programming, 10, 147-175, 1976.
